Le chiffrement par bloc
Deux grandes catégories :
La différence essentielle se situe sur la taille de bloc entre 32 et 512 bits.
Chiffrement symétrique
Anciennement le standard était le DES sur 64 bit,
il a été remplacé en 2000 par le standard AES sur 128 bits
Chiffrement par flot.
Il est possible de transformer un chiffrement de bloc en un chiffrement par flot
en utilisant un mode d'opération comme ECB (chaque bloc chiffré indépendamment
des autres) ou CFB (on chaîne le chiffrement en effectuant un XOR entre les
résultats successifs).
l'Advanced Encryption Standard (AES)
L'algorithme Rijndael a été conçu par deux chercheurs belges qui sont Joan Daemen et Vincent Rijmen pour devenir le successeur de l'algorithme DES.
L'objectif de l'AES se résume en trois points:
- Une résistance à tout type d'attaque et à la cryptoanalyse
- Une simplicité de conception
- Une grande rapidité du code selon l'optimisation de l'implémentation sur les plate-formes.
Fonctionnement
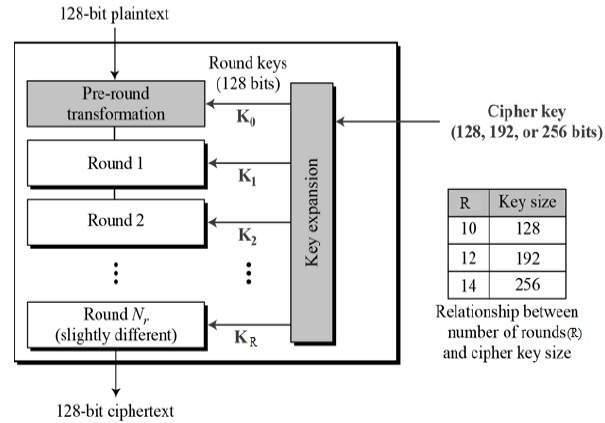
L'algorithme travaille sur des blocs plaintext P de 128 bits et les convertir en blocs Ciphers C de 128 bits selon un nombre de tours (10,12,14) qui peut être exécuter en séquence en fonction d'une clé d'une taille variable pouvant aller de 128,196,256 bits.
Nombre de tour
Selon la taille de la clé le nombre de tours évolue
Key length
128bits nk=4 196bits nk=6 256bits nk=8
Block Length
128 bits nb=4 10 12 14
196 bits nb=6 12 12 14
256 bits nb=8 14 14 14
Expansion de la clé
Après avoir subi une extension (Key Expansion), la clé sera découpée en sous-clés (appelées clés de tour),
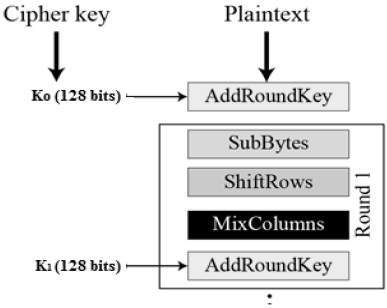
Processus de chiffrement d'un tour (Ki)
Byte Substitution (SubBytes)
Les 16 octets d'entrée sont substitués en recherchant une table fixe (S-box). Le résultat est une matrice de quatre rangées et quatre colonnes.
ShiftRows
Chacune des quatre rangées de la matrice est décalée vers la gauche. Toutes les entrées qui sortent à gauche sont réinsérés sur le côté droit de la ligne.
Selon la méthode effectuée comme suit: -
- La première rangée n'est pas décalée.
- La deuxième rangée est décalée d'une position (octet) vers la gauche.
- La troisième rangée est décalée de deux positions vers la gauche.
- La quatrième rangée est décalé de trois positions vers la gauche.
- Le résultat est une nouvelle matrice constituée par les mêmes 16 octets, mais décalé par rapport à l'autre.
MixColumns
Chaque colonne de quatre octets est maintenant transformé en utilisant une fonction mathématique particulière.
Cette fonction prend en entrée les quatre octets d'une colonne et quatre nouveaux octets en sorties qui remplacent la colonne d'origine.
Le résultat est une nouvelle matrice constituée de 16 octets. Il convient de noter que cette étape ne sera pas réalisée dans le dernier tour.
AddRoundKey
Les 16 octets de la matrice sont désormais considérés comme 128 bits et sont XORés aux 128 bits de la clé de tour .
Note: A chaque tour, une clé de tour est générée à partir de la clé secrète par un sous-algorithme (dit de cadencement). Cette clé de tour est ajoutée par un ou exclusif au dernier bloc obtenu.
Note: A chaque tour, une clé de tour est générée à partir de la clé secrète par un sous-algorithme (dit de cadencement). Cette clé de tour est ajoutée par un ou exclusif au dernier bloc obtenu.
Si c'est le dernier tour, alors le résultat est le cryptogramme. Sinon, les 128 bits résultants sont interprétés comme 16 octets et nous recommençons un autre tour similaire.
Rijndael_key_schedule
Rijndael_key_schedule
Processus de déchiffrement
Le processus de déchiffrement d'un cryptogramme AES est similaire au processus de chiffrement mais éxécuter dans l'ordre inverse. Chaque tour se compose des quatre processus .
Ajouter une clé de tour
Ajouter une clé de tour
- Mélanger les colonnes
- Le décalage lignes
- la substitution d'octet
Depuis les sous-processus, a chaque tour exécuté, les algorithmes de chiffrement et de déchiffrement doit être mis en œuvre séparément, bien qu'ils sont très étroitement liés.
Peudo code
Encryption Algorithm (128-bit version)
Cipher(byte in[16], byte out[16], word w[44]) begin byte state[4,4] state = in AddRoundKey(state, w[0, 3]) for round = 1 step 1 to 10 SubBytes(state) ShiftRows(state) MixColumns(state) AddRoundKey(state, w[round*4, (round+1)*4-1]) end for SubBytes(state) ShiftRows(state) AddRoundKey(state, w[40, 43]) out = state end
Advanced Encryption Standard
Rijndael_Animation
C AES encrypt/decrypt
AES_Decrypt.cpp
AES_Encrypt.cpp
voir exemple java ci-dessous :
Code Main Test
package test;
public class TestAES {
public static void main(String[] args) {
String key = "2efa3ec8dab164f3";
String plainText = "bonjour ceci est un test AES";
try{
//AES key 16 bytes, 128 bits
System.out.println("Text en clair plainText: "+plainText);
byte[] encryptedData = AES.encrypt128(plainText.getBytes(), key.getBytes());
System.out.println("Test chiffrement avec AES: {"+new String(encryptedData)+"]");
byte[] decrypteData = AES.decrypt128(encryptedData, key.getBytes());
System.out.println("Test dechiffrement avec AES: ["+new String(decrypteData)+"]" );
}catch(Exception e){
e.printStackTrace();
}
}
}
Java Code Exemple AES 128, il est possible de faire évoluer en 196 bits, 256bits, selon la taille de clé, le nombre de tour et la taille du bloc. Cet exemple est inspiré de divers autres exemples écrit en C que j'ai mis au point.
public class AES {
/* Nb: number bloc * Nk: number subkey * Nr: round number */
private static int Nb, Nk, Nr;
private static byte[][] roundKey;
private static final int DATA_BLOC_SIZE = 16;
private static final int KEY_SIZE = 16;
/* * S_BOX encrypt */
private static int[] sbox = {0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F,
0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76, 0xCA, 0x82,
0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C,
0xA4, 0x72, 0xC0, 0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC,
0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15, 0x04, 0xC7, 0x23,
0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27,
0xB2, 0x75, 0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52,
0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84, 0x53, 0xD1, 0x00, 0xED,
0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58,
0xCF, 0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9,
0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8, 0x51, 0xA3, 0x40, 0x8F, 0x92,
0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E,
0x3D, 0x64, 0x5D, 0x19, 0x73, 0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A,
0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB, 0xE0,
0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62,
0x91, 0x95, 0xE4, 0x79, 0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E,
0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08, 0xBA, 0x78,
0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B,
0xBD, 0x8B, 0x8A, 0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E,
0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E, 0xE1, 0xF8, 0x98,
0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55,
0x28, 0xDF, 0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41,
0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16};
/* * * S-box decrypt */
private static int[] inv_sbox = {0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5,
0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB, 0x7C, 0xE3,
0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4,
0xDE, 0xE9, 0xCB, 0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D,
0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E, 0x08, 0x2E, 0xA1,
0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B,
0xD1, 0x25, 0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4,
0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92, 0x6C, 0x70, 0x48, 0x50,
0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D,
0x84, 0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4,
0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06, 0xD0, 0x2C, 0x1E, 0x8F, 0xCA,
0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF,
0xCE, 0xF0, 0xB4, 0xE6, 0x73, 0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD,
0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E, 0x47,
0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E,
0xAA, 0x18, 0xBE, 0x1B, 0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79,
0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4, 0x1F, 0xDD,
0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27,
0x80, 0xEC, 0x5F, 0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D,
0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF, 0xA0, 0xE0, 0x3B,
0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53,
0x99, 0x61, 0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1,
0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D};
/* * sub key generation data */
public static int Rcon[] = {0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8, 0xab, 0x4d, 0x9a,
0x2f, 0x5e, 0xbc, 0x63, 0xc6, 0x97, 0x35, 0x6a, 0xd4, 0xb3, 0x7d, 0xfa, 0xef, 0xc5, 0x91, 0x39,
0x72, 0xe4, 0xd3, 0xbd, 0x61, 0xc2, 0x9f, 0x25, 0x4a, 0x94, 0x33, 0x66, 0xcc, 0x83, 0x1d, 0x3a,
0x74, 0xe8, 0xcb, 0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8,
0xab, 0x4d, 0x9a, 0x2f, 0x5e, 0xbc, 0x63, 0xc6, 0x97, 0x35, 0x6a, 0xd4, 0xb3, 0x7d, 0xfa, 0xef,
0xc5, 0x91, 0x39, 0x72, 0xe4, 0xd3, 0xbd, 0x61, 0xc2, 0x9f, 0x25, 0x4a, 0x94, 0x33, 0x66, 0xcc,
0x83, 0x1d, 0x3a, 0x74, 0xe8, 0xcb, 0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1b,
0x36, 0x6c, 0xd8, 0xab, 0x4d, 0x9a, 0x2f, 0x5e, 0xbc, 0x63, 0xc6, 0x97, 0x35, 0x6a, 0xd4, 0xb3,
0x7d, 0xfa, 0xef, 0xc5, 0x91, 0x39, 0x72, 0xe4, 0xd3, 0xbd, 0x61, 0xc2, 0x9f, 0x25, 0x4a, 0x94,
0x33, 0x66, 0xcc, 0x83, 0x1d, 0x3a, 0x74, 0xe8, 0xcb, 0x8d, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20,
0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8, 0xab, 0x4d, 0x9a, 0x2f, 0x5e, 0xbc, 0x63, 0xc6, 0x97, 0x35,
0x6a, 0xd4, 0xb3, 0x7d, 0xfa, 0xef, 0xc5, 0x91, 0x39, 0x72, 0xe4, 0xd3, 0xbd, 0x61, 0xc2, 0x9f,
0x25, 0x4a, 0x94, 0x33, 0x66, 0xcc, 0x83, 0x1d, 0x3a, 0x74, 0xe8, 0xcb, 0x8d, 0x01, 0x02, 0x04,
0x08, 0x10, 0x20, 0x40, 0x80, 0x1b, 0x36, 0x6c, 0xd8, 0xab, 0x4d, 0x9a, 0x2f, 0x5e, 0xbc, 0x63,
0xc6, 0x97, 0x35, 0x6a, 0xd4, 0xb3, 0x7d, 0xfa, 0xef, 0xc5, 0x91, 0x39, 0x72, 0xe4, 0xd3, 0xbd,
0x61, 0xc2, 0x9f, 0x25, 0x4a, 0x94, 0x33, 0x66, 0xcc, 0x83, 0x1d, 0x3a, 0x74, 0xe8, 0xcb};
public static byte[] xor(byte[] a, byte[] b) {
byte[] out = new byte[a.length];
for (int i = 0; i < a.length; i++)
out[i] = (byte) (a[i] ^ b[i]);
return out;
}
public static byte[][] KeyExpansion(byte[] key) {
int i, j;
byte[] temp;
byte k;
byte[][] roundKey = new byte[Nb * (Nr + 1)][4];
// premier tour, decompose la clé en sous partie de de 4 bytes
for (i = 0; i < Nk; i++) {
roundKey[i][0] = key[i * 4];
roundKey[i][1] = key[i * 4 + 1];
roundKey[i][2] = key[i * 4 + 2];
roundKey[i][3] = key[i * 4 + 3];
}
// calcul des sous clés pour tous les autre tours, // substitution de sous cle via un xor avec les bytes de la sbox
while (i < (Nb * (Nr + 1))) {
temp = new byte[4];
for (j = 0; j < 4; j++)
temp[j] = roundKey[i - 1][j];
if (i % Nk == 0) {
RotWord(temp);
temp = SubWord(temp);
temp[0] = (byte) (temp[0] ^ (Rcon[i / Nk] & 0xff));
} else if (Nk > 6 && i % Nk == 4) {
temp = SubWord(temp);
}
roundKey[i] = xor(roundKey[(i - Nk)], temp);
i++;
}
return roundKey;
}
public static void RotWord(byte[] temp) {
byte k;
k = temp[0];
temp[0] = temp[1];
temp[1] = temp[2];
temp[2] = temp[3];
temp[3] = k;
}
public static byte[] SubWord(byte[] in) {
byte[] tmp = new byte[in.length];
for (int i = 0; i < tmp.length; i++)
tmp[i] = (byte) (sbox[in[i] & 0x000000ff] & 0xff);
return tmp;
}
public static byte[][] AddRoundKey(byte[][] state, byte[][] roundKey, int round) {
int i, j;
for (i = 0; i < 4; i++) {
for (j = 0; j < 4; j++)
state[i][j] = (byte) (state[i][j] ^ roundKey[round * Nb + i][j]);
}
return state;
}
public static byte[][] SubBytes(byte[][] state) {
byte[][] tmp = state.clone();
int i, j;
for (i = 0; i < 4; i++) {
for (j = 0; j < 4; j++) {
state[i][j] = (byte) (byte) (sbox[(state[i][j] & 0x000000ff)] & 0xff);
}
}
return tmp;
}
public static byte[][] InvSubBytes(byte[][] state) {
byte[][] tmp = state.clone();
for (int row = 0; row < 4; row++)
for (int col = 0; col < Nb; col++)
tmp[row][col] = (byte) (inv_sbox[(tmp[row][col] & 0x000000ff)] & 0xff);
return tmp;
}
private static byte[][] ShiftRows(byte[][] state) {
byte[][] tmp = state.clone();
for (int r = 1; r < 4; r++) {
int j = 0;
byte[] t = new byte[4];
for (int c = 0; c < Nb; c++) {
t[j] = tmp[r][(c + r) % Nb];
j++;
}
tmp[r] = t;
}
return tmp;
}
private static byte[][] InvShiftRows(byte[][] state) {
byte[][] tmp = state.clone();
for (int r = 1; r < 4; r++) {
byte[] t = new byte[4];
for (int c = 0; c < Nb; c++)
t[(c + r) % Nb] = tmp[r][c];
for (int c = 0; c < Nb; c++)
tmp[r] = t;
}
return tmp;
}
private static byte[][] MixColumns(byte[][] s) {
int[] sp = new int[4];
byte b02 = (byte) 0x02, b03 = (byte) 0x03;
for (int c = 0; c < 4; c++) {
sp[0] = gMul(b02, s[0][c]) ^ gMul(b03, s[1][c]) ^ s[2][c] ^ s[3][c];
sp[1] = s[0][c] ^ gMul(b02, s[1][c]) ^ gMul(b03, s[2][c]) ^ s[3][c];
sp[2] = s[0][c] ^ s[1][c] ^ gMul(b02, s[2][c]) ^ gMul(b03, s[3][c]);
sp[3] = gMul(b03, s[0][c]) ^ s[1][c] ^ s[2][c] ^ gMul(b02, s[3][c]);
for (int i = 0; i < 4; i++) s[i][c] = (byte) (sp[i]);
}
return s;
}
private static byte[][] InvMixColumns(byte[][] s) {
int[] sp = new int[4];
byte b02 = (byte) 0x0e, b03 = (byte) 0x0b, b04 = (byte) 0x0d, b05 = (byte) 0x09;
for (int c = 0; c < 4; c++) {
sp[0] = gMul(b02, s[0][c]) ^ gMul(b03, s[1][c]) ^ gMul(b04, s[2][c]) ^ gMul(b05, s[3][c]);
sp[1] = gMul(b05, s[0][c]) ^ gMul(b02, s[1][c]) ^ gMul(b03, s[2][c]) ^ gMul(b04, s[3][c]);
sp[2] = gMul(b04, s[0][c]) ^ gMul(b05, s[1][c]) ^ gMul(b02, s[2][c]) ^ gMul(b03, s[3][c]);
sp[3] = gMul(b03, s[0][c]) ^ gMul(b04, s[1][c]) ^ gMul(b05, s[2][c]) ^ gMul(b02, s[3][c]);
for (int i = 0; i < 4; i++) s[i][c] = (byte) (sp[i]);
}
return s;
}
public static byte gMul(byte a, byte b) { // Galois Field (256) Multiplication of two Bytes byte p = 0;
byte counter;
byte hi_bit_set;
for (counter = 0; counter < 8; counter++) {
if ((b & 1) != 0) {
p ^= a;
}
hi_bit_set = (byte) (a & 0x80);
a <<= 1;
if (hi_bit_set != 0) {
a ^= (byte) 0x1b; /* x^8 + x^4 + x^3 + x + 1 */ }
b >>= 1;
}
return p;
}
public static byte[] encryptDataBloc(byte[] in) {
byte[] tmp = new byte[in.length];
byte[][] state = new byte[4][Nb];
for (int i = 0; i < in.length; i++)
state[i / 4][i % 4] = in[i % 4 * 4 + i / 4];
state = AddRoundKey(state, roundKey, 0);
for (int round = 1; round < Nr; round++) {
state = SubBytes(state);
state = ShiftRows(state);
state = MixColumns(state);
state = AddRoundKey(state, roundKey, round);
}
state = SubBytes(state);
state = ShiftRows(state);
state = AddRoundKey(state, roundKey, Nr);
for (int i = 0; i < tmp.length; i++)
tmp[i % 4 * 4 + i / 4] = state[i / 4][i % 4];
return tmp;
}
public static byte[] decryptDataBloc(byte[] in) {
byte[] tmp = new byte[in.length];
byte[][] state = new byte[4][Nb];
for (int i = 0; i < in.length; i++)
state[i / 4][i % 4] = in[i % 4 * 4 + i / 4];
state = AddRoundKey(state, roundKey, Nr);
for (int round = Nr - 1; round >= 1; round--) {
state = InvSubBytes(state);
state = InvShiftRows(state);
state = AddRoundKey(state, roundKey, round);
state = InvMixColumns(state);
}
state = InvSubBytes(state);
state = InvShiftRows(state);
state = AddRoundKey(state, roundKey, 0);
for (int i = 0; i < tmp.length; i++)
tmp[i % 4 * 4 + i / 4] = state[i / 4][i % 4];
return tmp;
}
public static byte[] encrypt128(byte[] in, byte[] key) {
Nb = 4;
Nk = key.length / 4;
Nr = Nk + 6;
int lenght = 0;
byte[] padding = new byte[1];
int i;
lenght = DATA_BLOC_SIZE - in.length % DATA_BLOC_SIZE;
padding = new byte[lenght];
padding[0] = (byte) 0x80;
for (i = 1; i < lenght; i++)
padding[i] = 0;
byte[] tmp = new byte[in.length + lenght];
byte[] bloc = new byte[DATA_BLOC_SIZE];
roundKey = KeyExpansion(key);
int count = 0;
for (i = 0; i < in.length + lenght; i++) {
if (i > 0 && i % DATA_BLOC_SIZE == 0) {
bloc = encryptDataBloc(bloc);
System.arraycopy(bloc, 0, tmp, i - DATA_BLOC_SIZE, bloc.length);
}
if (i < in.length)
bloc[i % DATA_BLOC_SIZE] = in[i];
else {
bloc[i % DATA_BLOC_SIZE] = padding[count % DATA_BLOC_SIZE];
count++;
}
}
if (bloc.length == DATA_BLOC_SIZE) {
bloc = encryptDataBloc(bloc);
System.arraycopy(bloc, 0, tmp, i - DATA_BLOC_SIZE, bloc.length);
}
return tmp;
}
/* * AES Decryt */ public static byte[] decrypt128(byte[] in, byte[] key) {
int i;
byte[] tmp = new byte[in.length];
byte[] bloc = new byte[DATA_BLOC_SIZE];
Nb = 4;
Nk = key.length / 4;
Nr = Nk + 6;
roundKey = KeyExpansion(key);
for (i = 0; i < in.length; i++) {
if (i > 0 && i % DATA_BLOC_SIZE == 0) {
bloc = decryptDataBloc(bloc);
System.arraycopy(bloc, 0, tmp, i - DATA_BLOC_SIZE, bloc.length);
}
if (i < in.length)
bloc[i % DATA_BLOC_SIZE] = in[i];
}
bloc = decryptDataBloc(bloc);
System.arraycopy(bloc, 0, tmp, i - DATA_BLOC_SIZE, bloc.length);
tmp = paddingClean(tmp);
return tmp;
}
private static byte[] paddingClean(byte[] input) {
int count = 0;
int i = input.length - 1;
while (input[i] == 0) {
count++;
i--;
}
byte[] tmp = new byte[input.length - count - 1];
System.arraycopy(input, 0, tmp, 0, tmp.length);
return tmp;
}
}
Console execution outputcom.intellij.rt.execution.application.AppMain test.TestAES
Text en clair plainText: bonjour ceci est un test AES
Test chiffrement avec AES: {�ܷ �� �� �Z����o ]�AQ#J�"��<1VQ]
Test dechiffrement avec AES: [bonjour ceci est un test AES]
Process finished with exit code 0
Aucun commentaire:
Enregistrer un commentaire