lundi 31 octobre 2016
04 - Algorithme pour l'authentification et l'intégrité - 2eme Partie (HMAC)
04 - Algorithme pour l'authentification et l'intégrité - 2eme Partie (HMAC)
MAC Message Authentication Code
Le MAC permet de vérifier l'intégrité d'un message, mais contrairement au SHA, le traitement de vérification n'est plus basé essentiellement sur le contenu du message. Il a été généré avec une clé secrète connu des entités émettrice et destinatrice, cela permet notamment d'authentifier l'expéditeur du message par le destinataire en plus de l'intégrité du contenu.
Un schéma wiki qui représente très simplement le traitement du MAC.
Authentification_de_message
HMAC keyed-hash message authentication code
Je pourrais résumé que Le HMAC est une implémentation basé sur le MAC et que cette fonction
peut être combiné avec différents algorithmes de hachage, HMAC-MD5, HMAC-SHA.
La qualité cryptographique dépend du choix de la fonction de hachage associé.
Exemple HMAC avec un SHA1 (wiki)
Keyed-Hash_Message_Authentication_Code
TODO
Lien utiles
Keyed-Hash_Message_Authentication_Code
Voir exemple ci-dessous
vendredi 28 octobre 2016
04 - Algorithme pour l'authentification et l'intégrité - 1ere Partie (SHA256)
Algorithmes pour l’authentification et l’intégrité - 1ere Partie (SHA256)
Une fonction de hachage génère une valeur condensée d'un ensemble de données pouvant être relativement volumineux.
C'est aussi une empreinte qui peut vérifier la signature concernant l'intégrité des données transmise.
Exemple, la vérification de la signature d'un fichier après téléchargement afin d'assurer qu'il n a pas été corrompu.
Cela permet également de conserver la confidentialité tel que les données personnelles d'un utilisateur qui doit conserver son anonymat dans le cadre des lois informatique et s'assurer de leur authenticité, (ex: téléphone mobile).
Les données générées par une fonction de hachage ne permettent pas de retrouver la donnée initiale.
Je ne vais pas prendre tous les algo de hachage, mais ceux que j'utilise, c'est à dire le SHA-256
et le HMAC, peut être du MD5 (à voir), avec un exemple que j'aurai écrit.
SHA-2 Secure Hash Algorithm
Les familles SHA sont écrits par la NSA (National Security Agency), La fonction de
hachage SHA-2 dérive des fonctions SHA-1, SHA-0,MD5, MD4
La famille SHA-2 fait référence aux algorithmes SHA224, SHA256, SHA384 et SHA512.
Pour les SHA-256 et SHA-512: Ces fonctions de hachage sont calculées avec
32-bits et 64-bits mots respectivement. Malgré l'utilisation de différentes quantités
de décalage et les constantes addictives, et leur structures, les deux sont presque
identiques. La seule différence réside dans le nombre de tours dans leurs structures.
Les attaques identifiées sur le SHA-1 n'ont pas pu être reproduite dans le cadre du SHA-2
SHA-1 SHA-256 SHA-384 SHA-512
Message digest size 160 256 384 512
Message size 2^64 2^64 2^128 2^128
Block size 512 512 1024 1024
Word size 32 32 64 64
Number of steps 80 80 80 80
Security 80 128 192 256
lien sur les spécificaitons de hachage
FIPS 180 - SECURE HASH STANDARD -
Le traitement se fait en deux étapes :
1) Pré Traitement, le message est complété avec des caractères de remplissage
pour être découper par bloc de 512 bits ou 64 bytes.
2) Le condensat s'obtient par un mécanisme de compression exécuté à chaque
itération dans la boucle de traitement des blocs du message qui aura été
préalablement découpé lors de la phase de pré-traitement.
6 fonctions logique sont utilisés :

Expression des formules en C
CH(x,y,z) (((x) & (y)) ^ (~(x) & (z)))
MAJ(x,y,z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z)))
EP0(x) (ROTRIGHT(x,2) ^ ROTRIGHT(x,13) ^ ROTRIGHT(x,22))
EP1(x) (ROTRIGHT(x,6) ^ ROTRIGHT(x,11) ^ ROTRIGHT(x,25))
SIG0(x)(ROTRIGHT(x,7) ^ ROTRIGHT(x,18) ^ ((x) >> 3))
SIG1(x)(ROTRIGHT(x,17)^ ROTRIGHT(x,19) ^ ((x) >> 10))
ROTRIGHT(a,b) (((a) >> (b)) | ((a) << (32-(b))))
ROTLEFT(a,b) (((a) << (b)) | ((a) >> (32-(b))))
Extrait de la fonction de hachage démontrant l'utilisation de ces formules.
La variable data contient le message.
int a, b, c, d, e, f, g, h, i, j, t1, t2; int[] m = new int[64];
int[] m = new int[64];
for (i = 0, j = 0; i < 16; ++i, j += 4) m[i] = (data[j] << 24) | (data[j + 1] << 16) | (data[j + 2] << 8) | (data[j + 3]);
for (; i < 64; ++i) m[i] = SIG1(m[i - 2]) + m[i - 7] + SIG0(m[i - 15]) + m[i - 16];
for (i = 0; i < 64; ++i) {
t1 = h + EP1(e) + CH(e, f, g) + k[i] + m[i];t1 = h + EP1(e) + CH(e, f, g) + k[i] + m[i];
t2 = EP0(a) + MAJ(a, b, c);t2 = EP0(a) + MAJ(a, b, c);
h = g;h = g;
g = f;g = f;
e = d + t1;e = d + t1;
f = e;f = e; d = c; a = t1 + t2; c = b; b = a;
}
Note: voir un exemple de traitement en java à la fin de cet article.
extrait du main :
byte[] data="hello world!".getBytes();
int strLen = data.length; SHA256_CTX ctx = new SHA256_CTX(); int[] hash = new int[32]; StringBuilder hashStr = new StringBuilder();
#Initialization Vector (en dur) SHA256Init(ctx);
#Pré traitement SHA256Update(ctx, data, strLen);
#hachage SHA256Final(ctx, hash);
# résultat du condensat sous forme texte for (int i = 0; i < 32; i++) hashStr.append(String.format("%02X", hash[i]));
return hashStr.toString();
Voici des schéma graphiques, Algo sha 256 (wiki), pour plus de détails : Traitement
Liens utiles
Fonction_de_hachage
SHA-2
sha256-hash-calculator
onewayhash
Voir exemple ci-dessous:
jeudi 27 octobre 2016
03 - Le chiffrement par bloc
Le chiffrement par bloc
Deux grandes catégories :
La différence essentielle se situe sur la taille de bloc entre 32 et 512 bits.
Chiffrement symétrique
Anciennement le standard était le DES sur 64 bit,
il a été remplacé en 2000 par le standard AES sur 128 bits
Chiffrement par flot.
Il est possible de transformer un chiffrement de bloc en un chiffrement par flot
en utilisant un mode d'opération comme ECB (chaque bloc chiffré indépendamment
des autres) ou CFB (on chaîne le chiffrement en effectuant un XOR entre les
résultats successifs).
l'Advanced Encryption Standard (AES)
L'algorithme Rijndael a été conçu par deux chercheurs belges qui sont Joan Daemen et Vincent Rijmen pour devenir le successeur de l'algorithme DES.
L'objectif de l'AES se résume en trois points:
- Une résistance à tout type d'attaque et à la cryptoanalyse
- Une simplicité de conception
- Une grande rapidité du code selon l'optimisation de l'implémentation sur les plate-formes.
Fonctionnement
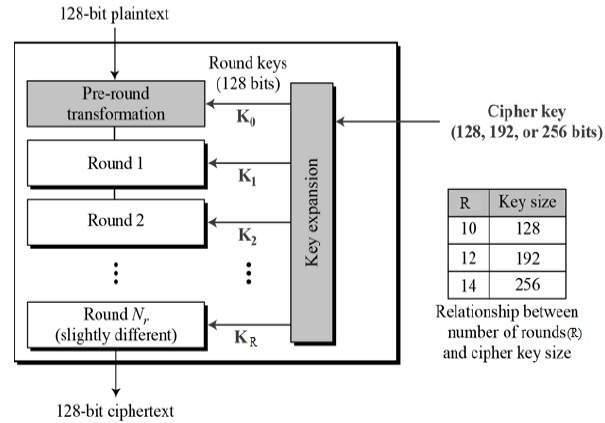
L'algorithme travaille sur des blocs plaintext P de 128 bits et les convertir en blocs Ciphers C de 128 bits selon un nombre de tours (10,12,14) qui peut être exécuter en séquence en fonction d'une clé d'une taille variable pouvant aller de 128,196,256 bits.
Nombre de tour
Selon la taille de la clé le nombre de tours évolue
Key length
128bits nk=4 196bits nk=6 256bits nk=8
Block Length
128 bits nb=4 10 12 14
196 bits nb=6 12 12 14
256 bits nb=8 14 14 14
Expansion de la clé
Après avoir subi une extension (Key Expansion), la clé sera découpée en sous-clés (appelées clés de tour),
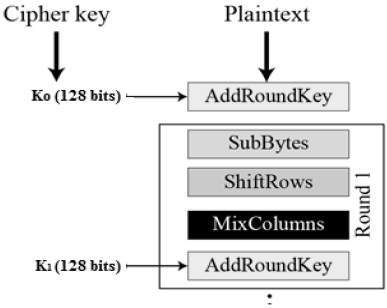
Processus de chiffrement d'un tour (Ki)
Byte Substitution (SubBytes)
Les 16 octets d'entrée sont substitués en recherchant une table fixe (S-box). Le résultat est une matrice de quatre rangées et quatre colonnes.
ShiftRows
Chacune des quatre rangées de la matrice est décalée vers la gauche. Toutes les entrées qui sortent à gauche sont réinsérés sur le côté droit de la ligne.
Selon la méthode effectuée comme suit: -
- La première rangée n'est pas décalée.
- La deuxième rangée est décalée d'une position (octet) vers la gauche.
- La troisième rangée est décalée de deux positions vers la gauche.
- La quatrième rangée est décalé de trois positions vers la gauche.
- Le résultat est une nouvelle matrice constituée par les mêmes 16 octets, mais décalé par rapport à l'autre.
MixColumns
Chaque colonne de quatre octets est maintenant transformé en utilisant une fonction mathématique particulière.
Cette fonction prend en entrée les quatre octets d'une colonne et quatre nouveaux octets en sorties qui remplacent la colonne d'origine.
Le résultat est une nouvelle matrice constituée de 16 octets. Il convient de noter que cette étape ne sera pas réalisée dans le dernier tour.
AddRoundKey
Les 16 octets de la matrice sont désormais considérés comme 128 bits et sont XORés aux 128 bits de la clé de tour .
Note: A chaque tour, une clé de tour est générée à partir de la clé secrète par un sous-algorithme (dit de cadencement). Cette clé de tour est ajoutée par un ou exclusif au dernier bloc obtenu.
Note: A chaque tour, une clé de tour est générée à partir de la clé secrète par un sous-algorithme (dit de cadencement). Cette clé de tour est ajoutée par un ou exclusif au dernier bloc obtenu.
Si c'est le dernier tour, alors le résultat est le cryptogramme. Sinon, les 128 bits résultants sont interprétés comme 16 octets et nous recommençons un autre tour similaire.
Rijndael_key_schedule
Rijndael_key_schedule
Processus de déchiffrement
Le processus de déchiffrement d'un cryptogramme AES est similaire au processus de chiffrement mais éxécuter dans l'ordre inverse. Chaque tour se compose des quatre processus .
Ajouter une clé de tour
Ajouter une clé de tour
- Mélanger les colonnes
- Le décalage lignes
- la substitution d'octet
Depuis les sous-processus, a chaque tour exécuté, les algorithmes de chiffrement et de déchiffrement doit être mis en œuvre séparément, bien qu'ils sont très étroitement liés.
Peudo code
Encryption Algorithm (128-bit version)
Cipher(byte in[16], byte out[16], word w[44]) begin byte state[4,4] state = in AddRoundKey(state, w[0, 3]) for round = 1 step 1 to 10 SubBytes(state) ShiftRows(state) MixColumns(state) AddRoundKey(state, w[round*4, (round+1)*4-1]) end for SubBytes(state) ShiftRows(state) AddRoundKey(state, w[40, 43]) out = state end
Advanced Encryption Standard
Rijndael_Animation
C AES encrypt/decrypt
AES_Decrypt.cpp
AES_Encrypt.cpp
voir exemple java ci-dessous :
lundi 24 octobre 2016
02 - Notions de base
Concepts Cryptographique
Comme cité dans l'article précédent, j'avais dit que la cryptographie était l'art de protéger un message en s'assurant de sa confidentialité, de son authenticité, de son intégrité, nous allons voir ces 3 notions.
Confidentialité:
Les données ne sont connues que des entités communicantes
C'est la mis en oeuvre d'un crypto système qui va gérer le chiffrement du message.
Crypto Système: M=Message, C=Chiffrer, K clé , H hash
Confidentialité par un système symétrique,
La même clé est utilisée pour Ek(M) et Dk(C).
Ce type de chiffrement nécessite un échange sûr
préalable de la clé K entre les entités A et B.
clé K chiffrement clé K déchiffrement
(A) ! ! (B)
M=>algo=>C ---------------->> C=>algo=>M
Confidentialité d’un système asymétrique,
Chaque entité possède sa propre paire de clés.
On aura donc la paire PkA, SkA pour l’entité A
et la paire PkB, SkB pour l’entité B.
Pk Public Key, Sk Secret Key
Chaque entité expéditrice utilise la public key de l'autre entité pour chiffrer C un message M, l'entité destinatrice déchiffre C avec sa clé secrète et récupère M.
clé PkB chiffrement clé SkB déchiffrement
(A) ! ! (B)
M=>algo=>C ----------------->> C=>algo=>M
Confidentialité d’un système hybride,
Avec le système à clé publique, on sécurise l’échange de la clé K (clé de session).
Les deux parties ayant acquis de manière sécurisée la clé de chiffrement K , On utilisera le système à clé symétrique pour chiffrer le message.
Génération clé K ( clé de session)
clé PkB chiffrement clé SkB déchiffrement
(A) ! ! (B)
K=>algo=>PkB(K) ----------->> PkB(K)=>algo=>K
clé K chiffrement clé K déchiffrement
(A) ! ! (B)
M=>algo=>C ------------------>> C=>algo=>M
Nous verrons un exemple concret d'échange dans un prochain article.
Garantir l’identité d’une entité
- Authentification par chiffrement (somme de contrôle)
- Authentification par hashage
- Authentification par MAC
MAC,Message Authentication Code) est un code accompagnant des
données dans le but d'assurer l'intégrité de ces dernières, en permettant
de vérifier qu'elles n'ont subi aucune modification, après une transmission
par exemple.
Au niveau des parties communicantes
Authentification symetrique
Ra est un nombre aléatoire, propre à l’utilisateur A.
A et B sont des identifiants personnels
A B
Generation Ra ======Ra========> E(Ra',B)
Dk ( E(Ra',B) ) <=== E(Ra',B) Rb=== Generation Rb
Ek(Rb,A) ==== Ek(Rb,A) ===> Dk ( Ek(Rb,A) )
Authentification asymetrique
L'expéditeur utilise la clé privé pour le chiffrement du message
Le destinataire ayant la clé publique peut vérifier l'authenticité du message
La confidentialité ne s'applique dans ce contexte.
A B
clé de chiffrement clé de déchiffrement
SkA PkA
! !
A-->algo--->C ====A|C======> C==algo) =====>A' A===========> ?=? comparaison
Au niveau du message
Authentification par MAC et syteme Symetrique
La clé secrète K utilisée étant partagée par les deux entités A et B.
Le MAC prend les dernier chiffres de C caclulés avec algo sur M et K
Le Message M et le MAC est envoyé au destinataire
L’authentification repose sur l’utilisation de la clé K.
Le MAC' est reconstitué des derniers chiffres de C avec algo sur M et K
Le MAC envoyé est vérifié avec le MAC' recalculer par le destinataire
(A) (B)
/------------- M
/ !
M / K===> algo
\ =algo => C =>MAC===>M|MAC==>/ !
/ \ C
K \ !
\- MAC ?=? MAC' comparaison
Authentification par MAC et hashage
La clé secrète K utilisée étant partagée par les deux entités A et B.
Le MAC est caclulé avec le hash sur le message M avec clé K par l'expéditeur
Le Message M et le MAC est envoyé au destinataire
L’authentification repose sur l’utilisation de la clé K.
Le MAC' est recalculé côté destinataire sur le message M avec clé K
Le MAC envoyé est vérifié avec le MAC' recalculer par le destinataire
(A) (B)
/------------- M
/ !
M / K===> Hash
\ =Hash===> MAC ===>M|MAC==>/ !
/ \- MAC ?=? MAC' comparaison
K
Authentification par signature
On fait abstraction de la confidentialité. C’est l’authentification qui importe.
L'expéditeur calcul le hash du Message M
On signe avec la clé privé SkA de l'expéditeur le hash H(M)
L'expéditeur envoi le message M et la signature au destinataire
Le destinataire recalcul H(M)' le Hash du Message M
Le destinataire récupère le hash H(M) venant de l'expéditeur avec la PkA
Le destinataire vérifie la valeur de hash H(M) avec le hash recalculer H(M)'
---------- M
/ !
/ Hash H(M)'
/ ? =? comparaison
M=>Hash H(M) => algo=>sign =>M|sign=>/ Hash H(M)
/ \ !
SkA \ PkA =>algo
\ !
\------- sign
Intégrité:
S'assurer que les message n'a pas subi de modification entre les entités communicantes
Envoi du message
M ================> M => Hash H(M)'
!
(A) (B) !
!
Hash H(M) ================> Hash H(M) ?=?' comparaison .
Une valeur de hashage se calcul rapidement
Une valeur de hashage ne permet pas de retrouver sa valeur initiale
Un message ne peut être modifier sans recalculer sa valeur de hashage
Deux message différents ne peuvent pas avoir la même valeur de hashage.
01- Mon Introduction
Etat de l'art sur ma perception de la cryptographie
Introduction
Bien, par quoi je commence ? tout simplement par le début, d'abord je ne suis pas un cryptographe de formation, ni un grand matheux. Tout ce que j'ai appris vient d'un investissement personnel car je suis de nature curieux et j'aime bien arriver à comprendre par beaucoup de pratique et un peu de théorie.
Je suis tombé dans le milieu de la cryptographie alors que j'ai une expérience qui n'a rien à voir avec ce monde, ces derniers temps j'étais surtout intéressé par le monde du big data et j'ai investi énormément d'énergie, mais une opportunité de carrière s'est présenté pour intégrer une connaissance et une expérience nouvelle qui m'a fait prendre un long détour auquel je ne m'attendais pas, mais on ne fait pas toujours ce qu'on veut, je le sais par expérience.
Quelle est ma motivation pour écrire ces articles, je fais cela pour m'obliger à m'investir dans la compréhension et l'usage de la cryptographie. Mon but n'est pas d'écrire un livre ou les RGS mais de faire ressortir de façon "simplifié" l'essentiel de ma compréhension. De fait, le premier lecteur sera moi.
Je ne désire pas devenir un cryptologue mais je souhaite être capable d'évoluer dans un monde ou la sécurité devient de plus en plus importante et complexe sur les autres sujets qui m'intéressent.
Mon approche est d'abord de présenter tous les articles sur des sujets que j'ai directement pratiqué, puis découvrir et pratiquer tous les autres sujets.
La cryptographie c'est quoi pour moi ? C'est l'art de protéger les messages en maîtrisant les techniques de confidentialité, d'authenticité, d'intégrité avec l'aide de secret ou de clé.
je reviendrais progressivement sur ces notions dans les articles suivants.
Mon premier contact avec la cryptographie se situe dans les années 90, j'avais besoin de gérer des codes d'accès, j'ai fini par découvrir le chiffre de César qui était relativement simple. Il était suffisant vu le niveau des connaissances utilisateurs de l'époque,
J'avais mis en oeuvre cette méthode pour chiffrer des codes à 8-10 lettres fourni par l'utilisateur ainsi que l'heure affichée, cela me permettait de retrouver la valeur aléatoire de décalage à appliquer pour donner la bonne réponse et permettre l'accès à des programmes sensible, cela afin d'éviter à certains utilisateurs de noter sur un cahier tous les codes d'accès à des programmes dédié à la maintenance.
Si j'obtiens une valeur aléatoire de 1 à 26 , exemple 3 et que la valeur à chiffrer est "SALUTATION"
Si 3 est la clé n à ajouter ou à soustraire sur la valeur du caractère x dans le cadre d'une permutation circulaire selon que l'on souhaite chiffre ou déchiffrer la valeur.
En(x) =(x+n)[26] ca donne un chiffré de: VDOXWDWLRQ pour la valeur "SALUTATION"
(1) En(x) V = S + 3
(2) En(x) D = A + 3
(3) En(x) O = L + 3
(4) En(x) X = U + 3
(5) En(x) W = T + 3
(6) En(x) D = A + 3
(7) En(x) W = T + 3
(8) En(x) L = I + 3
(9) En(x) R = O+ 3
(10) En(x) Q = N+ 3
(1) Dn(x) S = V - 3
(2) Dn(x) A = D - 3
(3) Dn(x) L = O - 3
(4) Dn(x) U = X - 3
(5) Dn(x) T = W- 3
(6) Dn(x) A = D - 3
(7) Dn(x) T = W- 3
(8) Dn(x) I = L - 3
(9) Dn(x) O = R - 3
(10) Dn(x)N = Q - 3
Cette méthode à une faille, si on regarde la répétition statistique des lettres du cryptogramme on peut arriver à retrouver le texte initiale.
Qui dit Chiffre de César, dit aussi Chiffre de Vigenère que j'ai découvert peu de temps après et qui me permettait d'améliorer le chiffre de César, j'ai pu renforcer mon mécanisme de code d'accès gràce à une clé permettant de calculer un décalage automatique selon le rang de la clé A=0,
B=1,C=2,...,Z=25
valeur à chiffrer SALUTATION
clé M O N S E C R E T
décalage 12 14 13 18 4 2 17 4 19
valeur chiffrée EOYMXCKMHZ
On obtient par cette méthode une meilleure répartition statistique du chiffrer concernant la répétition des lettres utiliser dans le cryptograme.
Le chiffre de Vigenère et le chiffre de César sont considérés comme des algorithmes de chiffrement faible; (facilement déchiffrable)
Je reviendrais plus tard sur ces sujets sur d'autres billets, notamment sur les attaques en force brute et les failles potentielles des crypto-systèmes.
On trouve de nombreux site pour tester, voici quelques liens.
Chiffre de César
http://www.nymphomath.ch/crypto/cesar/index.html
Chiffre de Vigenère
http://www.nymphomath.ch/crypto/vigenere/index.html
Très intéressant à décortiquer - Attaque et dechiffrement
Note : Faut que je regarde sur le blog si je peux intégrer du javascript, il est susceptible d'être revu au fur et à mesure de la progression de mes connaissances.
Voilà, c'est mon premier blog et c'est mon premier billet, j'ai mis le pied dedans et un long chemin commence avant d'arriver à ma conclusion,
Ci-Dessous mon livre de chevet, attention c'est une édition de 1996, il n'intègre pas le SHA-2 ou l'AES.
mais il est bien fait.
https://www.amazon.fr/Cryptographie-appliqu%C3%A9e-Bruce-Schneier/dp/2711786765/ref=sr_1_3?ie=UTF8&qid=1477337903&sr=8-3&keywords=cryptographie+appliqu%C3%A9
Inscription à :
Commentaires (Atom)